Pierre CRESPIN
Etude sur le quinzième pavage pentagonal du plan
Partie 2 AutresTuilesBlocs
Recherche d'autres tuiles-blocs pavant le plan et ayant les mêmes éléments de symétrie
Pierre CRESPIN |
Etude sur le quinzième pavage pentagonal du plan |
Partie 2 AutresTuilesBlocs |
Recherche d'autres tuiles-blocs pavant le plan et ayant les mêmes éléments de symétrie |
La découverte de trois pavages du plan (dont celui du type "pavage islamique") ayant les mêmes éléments de symétrie que le quinzième pavage pentagonal (par Penta15) m'a encouragé à rechercher d'autres tuiles-blocs sousjacentes au pavage "Penta15". D'autant plus que l'introduction assez naturelle de certains pavés-hexagones dans la première partie (nouveaux pour moi) ou d'autres pavés classiques m'a conduit à approfondir la recherche de leurs propriétés. |
||
 |
 |
 |
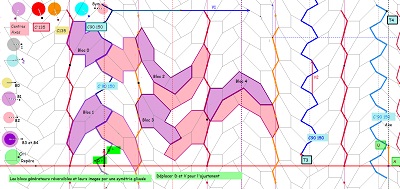
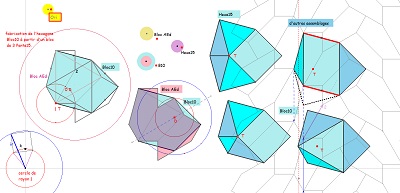
Poursuite de la recherche d'autres tuiles et les pavages leur correspondant, avec, en fin de cette liste, un hexagone que j'aurais du voir beaucoup plus tôt, appelé ici Bloc10 ou Hexa10, qui pave le plan bien sûr, et qui est assez proche de celui que j'ai appelé Hexa15, qui, lui, ne le pave pas. Il est ici, de proche en proche, descendant du bloc appelé Bloc3d constitué de 3 pavés Penta15 par symétries axiales. |
||
Sous Cabri, les nouveaux blocs et les pavages |
 |
|
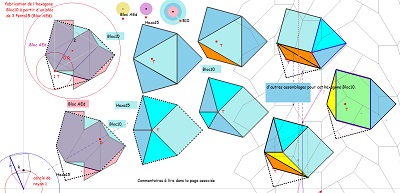
le pavage par Bloc10 (hexagone Hexa10) à rapprocher de celui par Bloc9 (octogone) |
 |
|
et quelques propriétés immédiates de ce Bloc10 ou Hexa10 |
avec d'autres polygones ou blocs de l'étude |
|
 |
 |
|
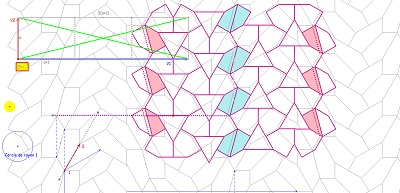
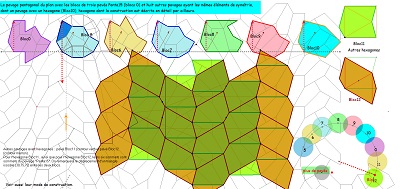
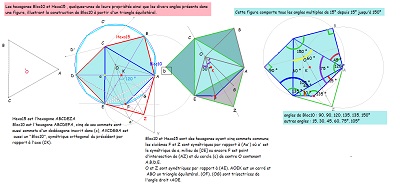
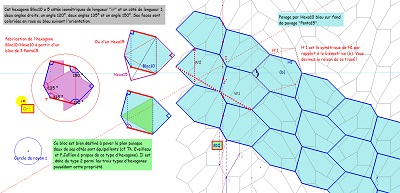
Outre le fait que cet hexagone est issu de l'hexagone Hexa15, il m'apparait, à partir de la construction autour d'un triangle équilatéral, comme employant tous les angles multiples de 15° depuis 15° jusqu'à 150°, propriété un peu artificielle, mais qui me tracassait depuis le début de l'étude. Possédant cinq côtés isométriques, et deux d'entre eux étant "équipollents", cet hexagone fait bien partie des 3 types d'hexagones qui pavent le plan. Nous utiliserons aussi, comme toujours, le pavé symétrique orthogonal ici coloré en rose |
 |
|
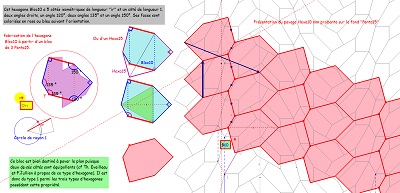
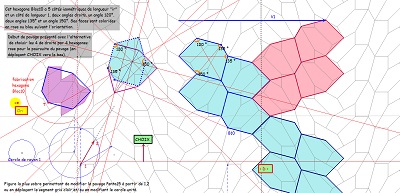
L'hexagone Bloc10/Hexa10 permet aussi d'autres pavages du plan, et même une infinité, en incluant ou non des colonnes bleu ou rose, dont les frontières (lignes brisées d'angles droits) sont les mêmes. |
||
 |
 |
 |
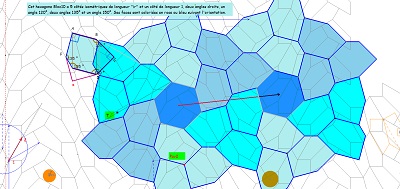
Et même des pavages à partir de rosaces ,utilisant des hexagones réguliers, pour un pavage que l'on ne peut appeler ni régulier ni semi-régulier, mais qui mériterait un nom. |
 |
|
S'ensuivent des tentatives diverses à partir de la constatation de la présence d'un triangle équilatéral inscrit dans cet hexagone, comme dans beaucoup d'autres déjà rencontrés, et à rapprocher des polygones de Haag (digression motivée par les documents du site de Pierre Audibert) et des activités motivées par les sites de David Bayley, Livio Zucca, ... certaines à propos des pavés de Marjorie Rice et des pentagones équilatéraux,
|
||
Suite ( Partie 2 -10 HexagonesRencontres) |
ou vers Conclusion Partie II |
|